The problem presented is that you have a one dimensional array of numbers. From that array you need to find the maximum sum sub-array. The sub-array must be contiguous.

The solution to this can be in several forms. You could just want the actual maximum sum of the numbers. In this case you would find the sub-array and then sum all of the numbers and return the value of the maximum sum. Another solution could be that you want the elements of the sub-array. Finally, perhaps you just need to provide the indices where the sub-array starts and ends.

There are several ways you can implement this solution.

• Brute-force. Just look at every possible combination and choose the best one.
• Divide and Conquer. This approach will divide the problem into a smaller problem and solve the smaller problems.
• Kadane's algorithm

Here we explore the Brute-Force method.

Brute Force Sum

Whenever I am trying create a solution, the brute-force method is one of the first things I do. It certainly is not the best, but it can be an effective way to better understand the problem and ensure you are getting a correct solution.

The concept behind the brute-force method is that you will just try all of the possible solutions until you are satisfied that you have the best.

Brute force algorithms are rarely the best. Sometimes they are the only method available for a problem. This is not the case for this problem though.

Using the array [-1, 3, -2, 3, -2, -1, 5, -4, -1] the maximum sum sub-array of [3, -2, 3, -2, -1, 5] starting at index 1 and ending at index 6 with a sum of 6.

A brute force approach to finding this value would be to iterate over the array and keeping track of each sub-array and the sum. If a sum is found that is higher you keep track of that.

maxSum=0
currentSum=0

for(i=0; i < array.length; i++)
{
  currentSum=0
  for(j=i; j < array.length; j++)
  {
    currentSum = currentSum + array[j];
    if(currentSum > maxSum)
    {
        maxSum = currentSum;
    }
  }
}
return maxSum;

In the pseudo-code we start at the first position in the array and reset the current sum. The first check inside the second loop looks at the value of the sub-array starting at index 0 and of a size of 1.

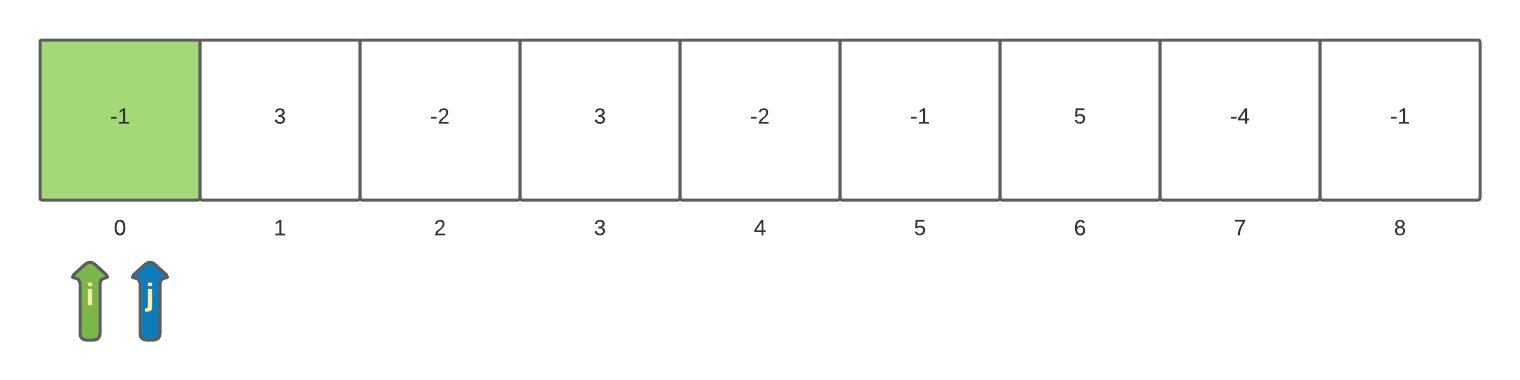
The first time through the loop with i=0 and j=0 the sum is -1. Since -1 is less than the current maxSum it will not be assigned to maxSum

The end index j will be incremented to 1 and point to the next element in the array. This increases the size of the current sub-array to 2.

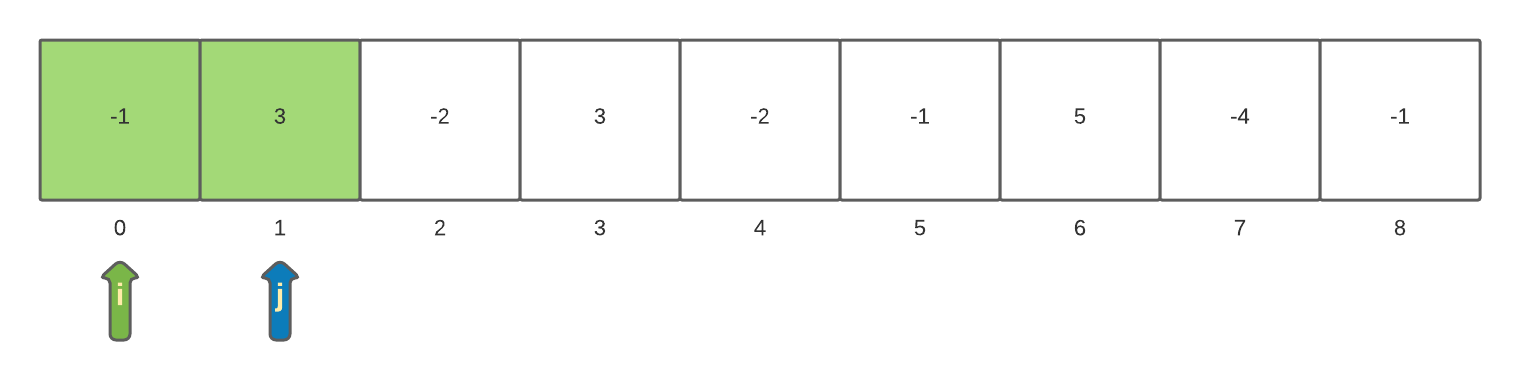
The value of the array[j] is now added to the currentSum and currentSum becomes 2. The currentSum is compared against the maxSum. Since the current currentSum is greater than the maxSum the maxSum is updated to be the value of currentSum.

The inner loop continues to increment the index value of j and add the value of array[j] to the currentSum. Each time the currentSum is incremented it is compared against the value of maxSum. If the value of currentSum is greater than maxSum it will become the new maxSum.

This results in the maxSum changing during the initial loop of j to 3 and then 5 before reaching the end of the array.

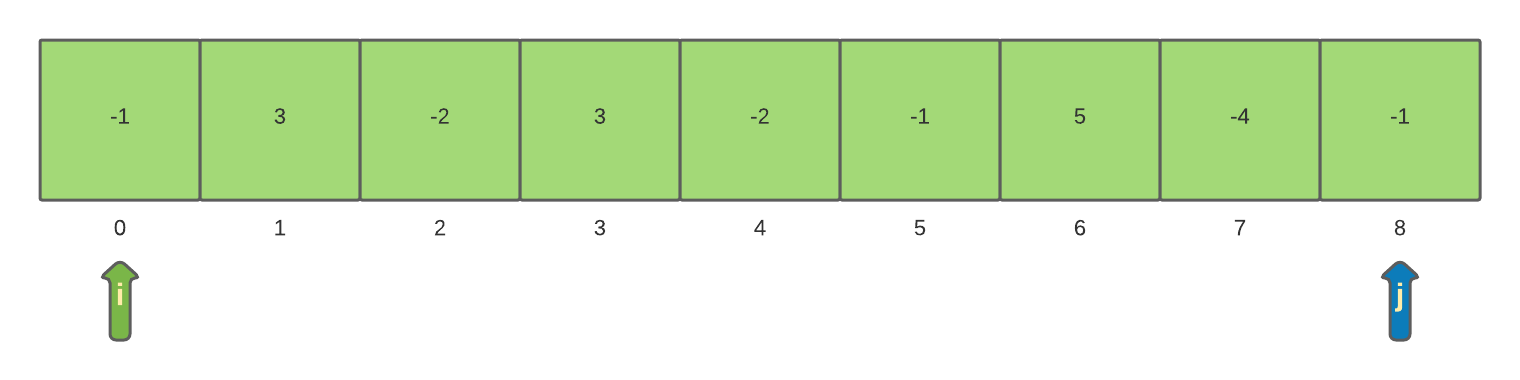
Now that the inner loop has completed to the end of the array the outer loop iterator i is incremented to 1 and the currentSum is reset to 0. At this time the maxSum is 5. Now the process of examining a sub-array and the sum resumes. However, this time the sub-array will start at position 1.

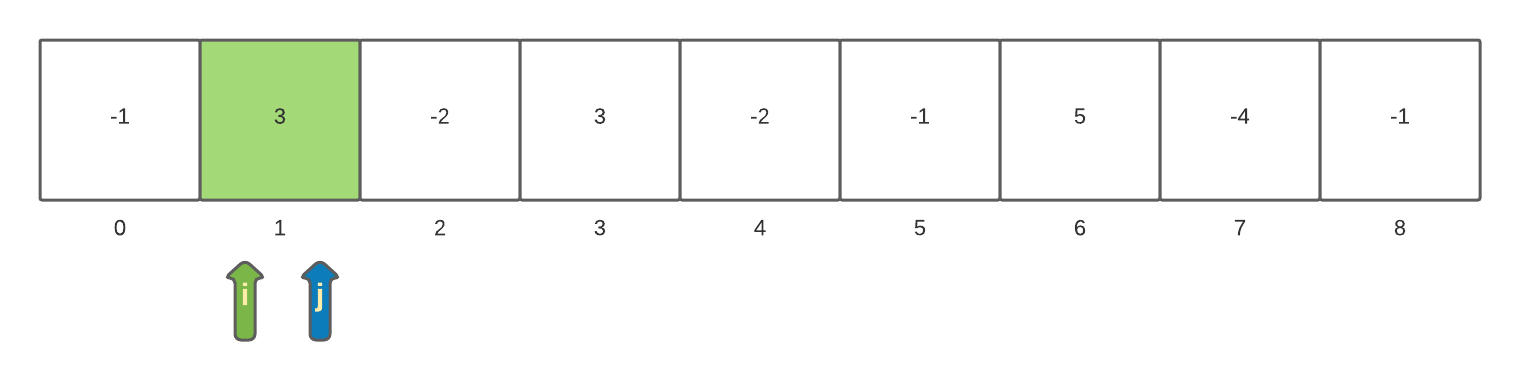
The process of incrementing the inner loop iterator and incrementing the currentSum will continue until the inner loop reaches the end of the array. When we reach the ending index inside the inner loop with a value of 6 we find the next maxSum of 6.

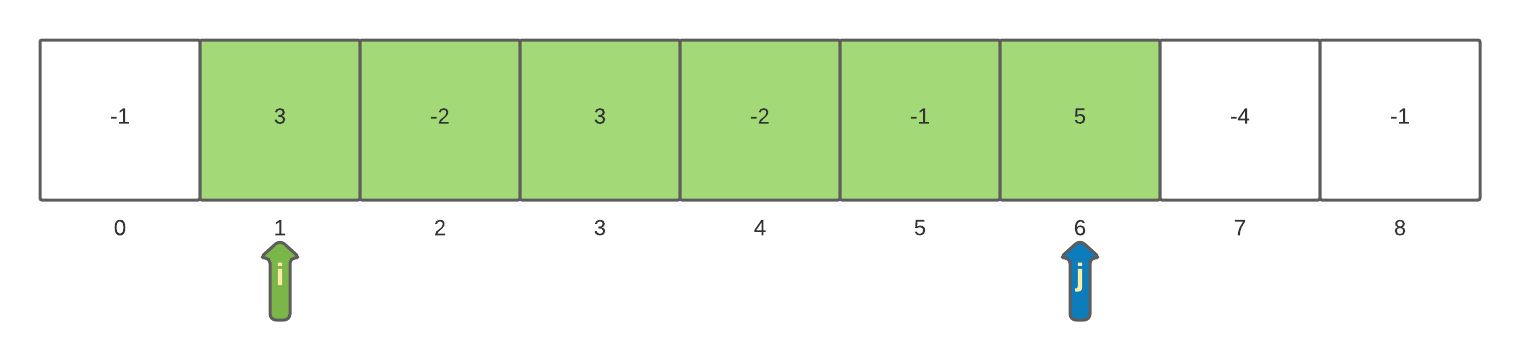
The inner loop continues to be incremented until it again reaches the end of the array. The final scan of a sub-array starting at index 1 results in a sub-array of size 8 with a maxSum of 6.

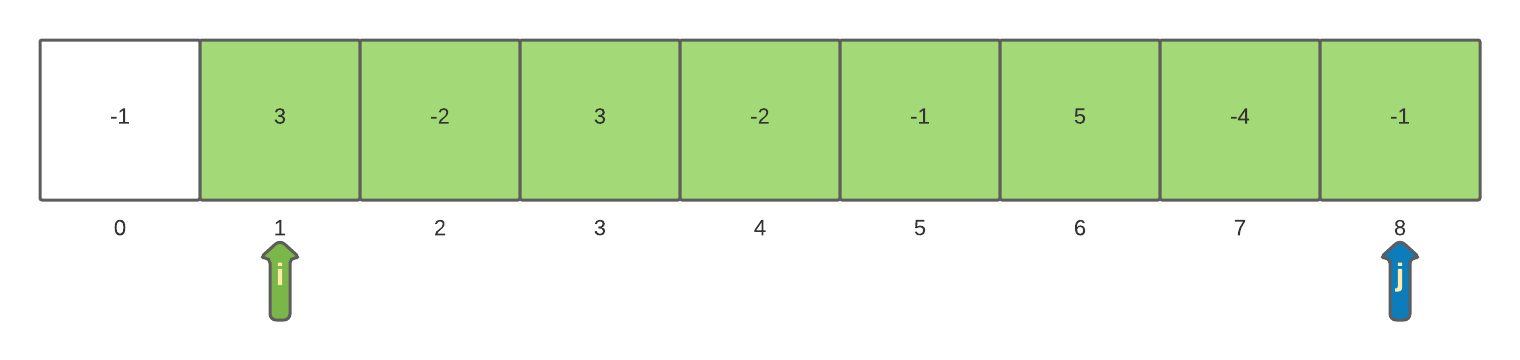
After the scanning the array with position 0 as the starting index and then scanning the array again with the starting position as 1 we have a new maxSum of 6.

The process of incrementing the staring index and then scanning the array until the end continues. Anytime a greater maxSum is found it is saved. Eventually the starting index will be incremented to the very last index in the array and the final sub-array to be tested will be a sub-array of size 1 starting at index 8.

At this point every possible sub-array has been tested and the maximum sum has been determined.

Analysis of Solution

The time complexity of the solution depends on the loops. The inner loop must iterate over the array N times. This means that the number of iterations depends on the number of elements in the array.

The outer most loop must also iterate over the array N times. Since the second loop is nested inside the outer loop this makes the complexity N*N. This is expressed as O(n^2).

The next thing to consider is the amount of space, or memory, that is required to complete the solution. In this solution we have to initialize a few variables, but the size of those variables is constant. The size of the incoming array is also constant. The amount of memory used in this solution remains constant during the entire process. This makes the space complexity O(1).

What about all negative numbers?

After running some sample data through this algorithm you might notice that there are some edge cases that do not work. The first one is when you have an array that contains all negative numbers. The current algorithm doesn't seem to handle it very well. It reports that the maxSum is zero depsite there being no way to have that value if all of the numbers are negative.

This can be easily fixed.

Instead of initializing the maxSum=0, initialize it to the minimum integer value possible.

maxSum=MIN_INT

This simple change will now allow the algorithm to properly report on an array that has all negative numbers.

What is the actual sub-array

Another aspect of the current algorithm is that you cannot actually report on what the sub-array is that provides the maximum sum. You only know what that sum is. By iterating through the example we can see that the maximum sub-array is actual the array starting at index 1 and ending at index 6.

To be able to provide this information as a result of the algorithm we need to make some minor changes. We need to track what the beginning and ending indexes are. We can do this by adding a few extra variables.

maxStartIndex = 0
maxEndIndex = 0

Initially we assign the values to zero. Each time we find a currentSum that is larger than the maxSum we assign the index values. This results in the outer loop iterator i being assigned to the maxStartIndex and the inner loop iterator j being assigned to maxEndIndex.

We now know at the end of all of the scans that the start and end index is for the sub-array that results in a maximum sum.

Using this information a new sub-array can be returned or just the indexes of the sub-array can be returned.