The problem presented is that you have a one dimensional array of numbers. From that array you need to find the maximum sum sub-array. The sub-array must be contiguous.

The solution to this can be in several forms. You could just want the actual maximum sum of the numbers. In this case you would find the sub-array and then sum all of the numbers and return the value of the maximum sum. Another solution could be that you want the elements of the sub-array. Finally, perhaps you just need to provide the indices where the sub-array starts and ends.

There are several ways you can implement this solution.

• Brute-force. Just look at every possible combination and choose the best one.
• Divide and Conquer. This approach will divide the problem into a smaller problem and solve the smaller problems.
• Kadane's algorithm.

Here we explore Kadane's algorithm.

Compute Maximum Sum

Presented with an array of numbers, find the maximum sum sub-array.

Kadane's algorithm is an optimized method of scanning the array to find the largest sum sub-array. Like the brute-force method it iterates over the array to find the maximum sum. However it does it using a single loop which improves the performance.

maxSum = 0
currentSum = 0

// Iterate over the array
for (i = 0; i < array.length; i++)
{
  // add current index to sum
  currentSum = currentSum + array[i]

  // Is the current sum less than zero?
  if(currentSum < 0)
  {
    // Reset the sum and subarray indexes.
    currentSum=0
  }
  if(currentSum > maxSum)
  {
    maxSum = currentSum;
  }
}
return maxSum
}

In addition to only having a single loop this algorithm has another change from the brute-force method. It resets the currentSum to zero if it ever drops below zero. This is the key to this algorithm. If the currentSum is ever less than zero then you can safely discard the entire sub-array that you have built up to this point. Any values to the left of the current position will only result in a smaller sum no matter how large the positive values are remaining in the array.

Finally, the currentSum is compared to the maxSum and a new maxSum is assigned if the currentSum is larger.

If we use our example array towalk through the algorithm this is what we see. First the iterator starts with position 0. This results in a sub-array of length 1 with a currentSum of -1

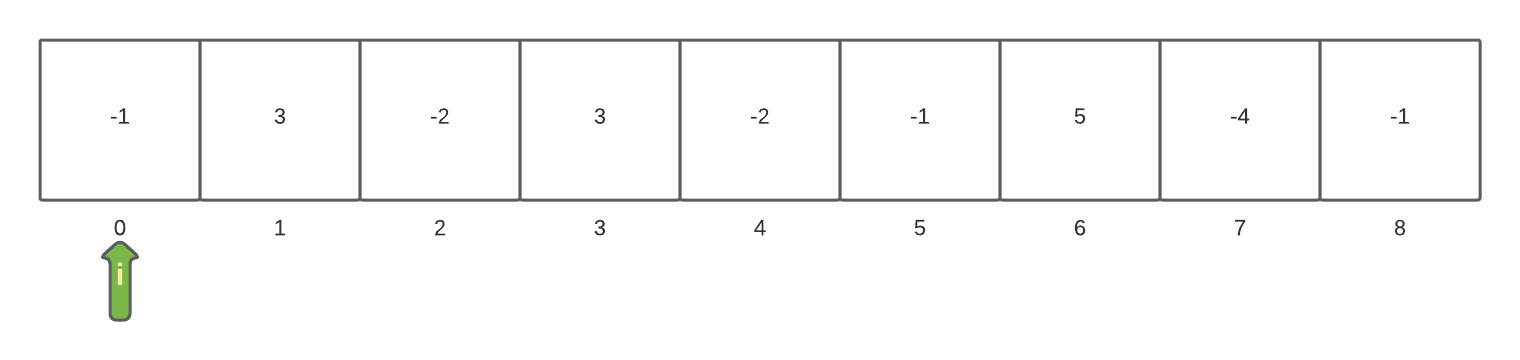
The currentSum is found to be less than zero and so the currentSum is reset to 0. Since the currentSum is not greater than the maxSum the loop continues and increments to the next item.

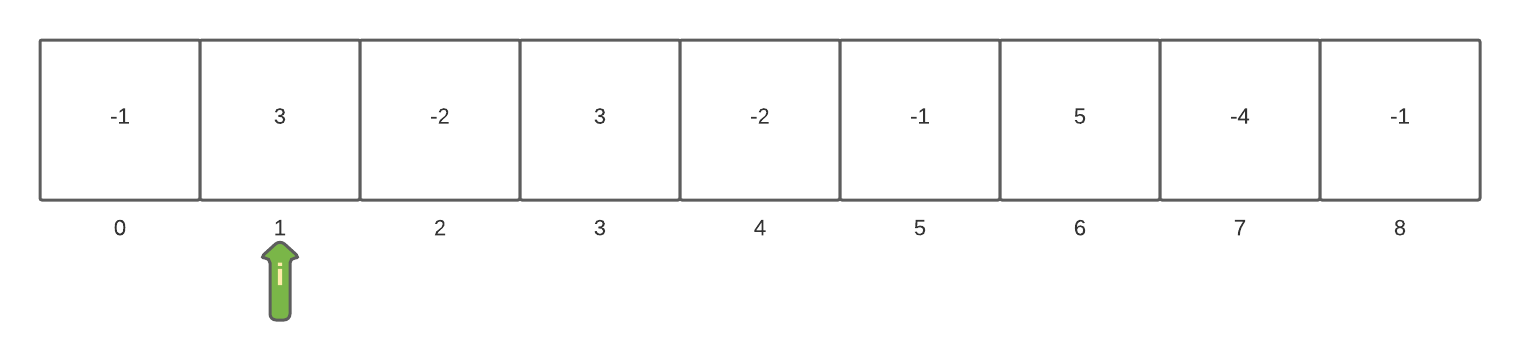
During the second time through the loop the array[i] value of 3 is examined. The currentSum is incremented by 3 resulting in a value of 3 since we reset the currentSum to zero during the previous loop. The currentSum is not less than zero so we do not need to reset it. The currentSum is greater than the current maxSum and so the maxSum is now set to the curentSum and the loop is incremented to the next element.

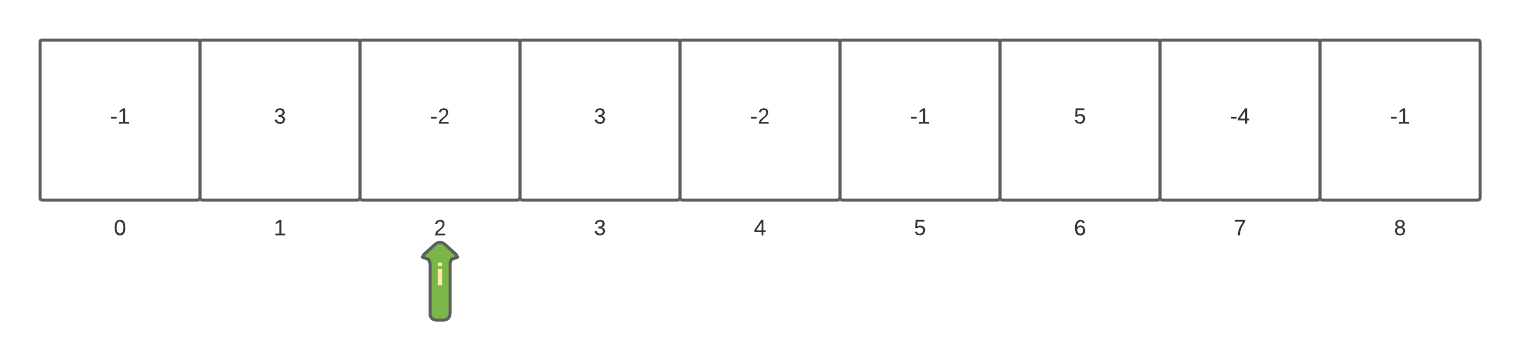
The array[2] is now being inspected. The value of this is added to the currentSum and results in a value of 1 since the value of currentSum is 3 and the value of array[i] is -2.

The loop continues to inspect the next element in the array and add it to the currentSum. Each time the currentSum is larger than the maxSum it is assigned to maxSum.

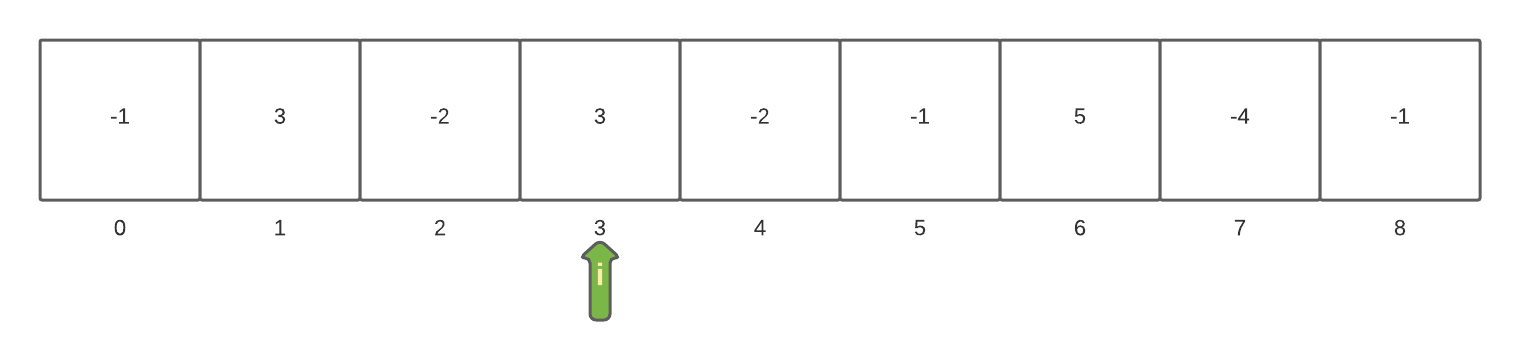
After reaching array[6] the maxSum is currently set to 6.

The array index is incremented to the next two elements array[7] and array[8]. Each time the currentSum is insepcted it is found that it is less than the maxSum. After inspecting all of the elements it has been determined that the maxSum is 6.

Analysis of solution

The solution must iterate over the entire array before it can determine the maximum sum. However it only needs to do this one. This means that the time for this algorithm to complete it will take N iterations. This results in a complexity of O(n).

Negative Numbers

The algorithm as it is presented will not work if all numbers in the array are negative or if the highest value item is a zero. A minor change to the algorithm can remedy this though. Set the initial maxSum to MIN_INT to represent the minimum value for an integer. Secondly, move the check for a currentSum less than zero to after the maxSum is set.

maxSum = MIN_INT
currentSum = 0

// Iterate over the array
for (i = 0; i < array.length; i++)
{
  // add current index to sum
  currentSum = currentSum + array[i]

  if(currentSum > maxSum)
  {
    maxSum = currentSum;
  }
  // Is the current sum less than zero?
  if(currentSum < 0)
  {
    // Reset the sum and subarray indexes.
    currentSum=0
  }
}
return maxSum
}

Now imagine an array where ALL of the values are MIN_INT. With the maxSum now set to the minimum value for an integer any value in the array is guaranteed to be greater than or equal to the maxSum. If the first value in the array is the MIN_INT then the maxSum will remain MIN_INT. The currentSum will be reset to 0. At each iteration, the value of currentSum will be found to be less than or equal to the maxSum and therefore the maxSum will not change.

After all of the array values have been inspected the maxSum of MIN_INT will be returned.

If there is an array where at least one of the values is greater than MIN_INT then the currentSum will be greater than maxSum and it will be set accordingly.

You now can compute the maximum sum sub-array in O(n) time and process an array with all negative values or a mix of negative and positive.