Blog

Problem

Given an dictionary with string values, find the longest string value in the dictionary.

Read more »

The problem presented is that you have a one dimensional array of numbers. From that array you need to find the maximum sum sub-array. The sub-array must be contiguous.

The solution to this can be in several forms. You could just want the actual maximum sum of the numbers. In this case you would find the sub-array and then sum all of the numbers and return the value of the maximum sum. Another solution could be that you want the elements of the sub-array. Finally, perhaps you just need to provide the indices where the sub-array starts and ends.

There are several ways you can implement this solution.

• Brute-force. Just look at every possible combination and choose the best one.
• Divide and Conquer. This approach will divide the problem into a smaller problem and solve the smaller problems.
• Kadane's algorithm.

Here we explore Kadane's algorithm.

Compute Maximum Sum

Presented with an array of numbers, find the maximum sum sub-array.

Kadane's algorithm is an optimized method of scanning the array to find the largest sum sub-array. Like the brute-force method it iterates over the array to find the maximum sum. However it does it using a single loop which improves the performance.

maxSum = 0
currentSum = 0

// Iterate over the array
for (i = 0; i < array.length; i++)
{
  // add current index to sum
  currentSum = currentSum + array[i]

  // Is the current sum less than zero?
  if(currentSum < 0)
  {
    // Reset the sum and subarray indexes.
    currentSum=0
  }
  if(currentSum > maxSum)
  {
    maxSum = currentSum;
  }
}
return maxSum
}

In addition to only having a single loop this algorithm has another change from the brute-force method. It resets the currentSum to zero if it ever drops below zero. This is the key to this algorithm. If the currentSum is ever less than zero then you can safely discard the entire sub-array that you have built up to this point. Any values to the left of the current position will only result in a smaller sum no matter how large the positive values are remaining in the array.

Finally, the currentSum is compared to the maxSum and a new maxSum is assigned if the currentSum is larger.

If we use our example array towalk through the algorithm this is what we see. First the iterator starts with position 0. This results in a sub-array of length 1 with a currentSum of -1

The currentSum is found to be less than zero and so the currentSum is reset to 0. Since the currentSum is not greater than the maxSum the loop continues and increments to the next item.

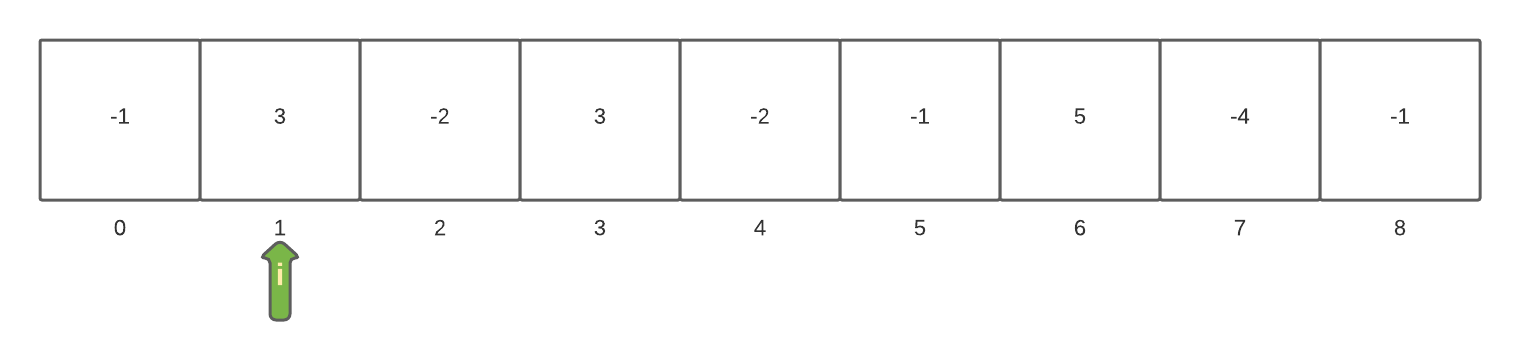
During the second time through the loop the array[i] value of 3 is examined. The currentSum is incremented by 3 resulting in a value of 3 since we reset the currentSum to zero during the previous loop. The currentSum is not less than zero so we do not need to reset it. The currentSum is greater than the current maxSum and so the maxSum is now set to the curentSum and the loop is incremented to the next element.

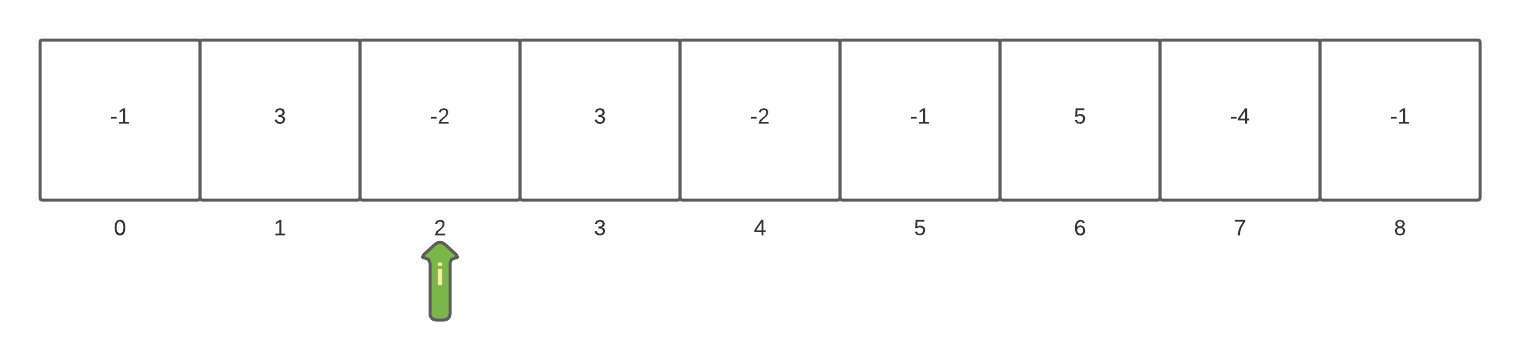
The array[2] is now being inspected. The value of this is added to the currentSum and results in a value of 1 since the value of currentSum is 3 and the value of array[i] is -2.

The loop continues to inspect the next element in the array and add it to the currentSum. Each time the currentSum is larger than the maxSum it is assigned to maxSum.

After reaching array[6] the maxSum is currently set to 6.

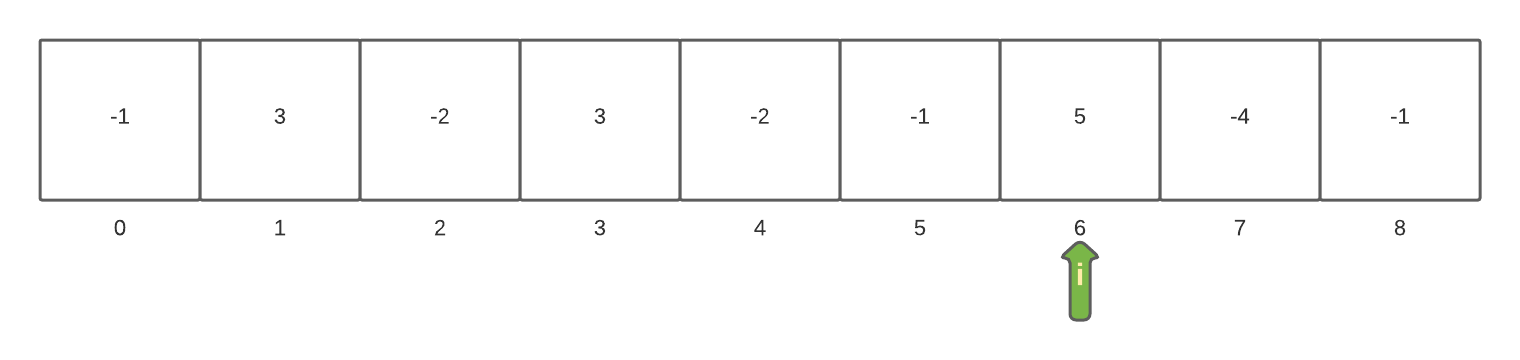
The array index is incremented to the next two elements array[7] and array[8]. Each time the currentSum is insepcted it is found that it is less than the maxSum. After inspecting all of the elements it has been determined that the maxSum is 6.

Analysis of solution

The solution must iterate over the entire array before it can determine the maximum sum. However it only needs to do this one. This means that the time for this algorithm to complete it will take N iterations. This results in a complexity of O(n).

Negative Numbers

The algorithm as it is presented will not work if all numbers in the array are negative or if the highest value item is a zero. A minor change to the algorithm can remedy this though. Set the initial maxSum to MIN_INT to represent the minimum value for an integer. Secondly, move the check for a currentSum less than zero to after the maxSum is set.

maxSum = MIN_INT
currentSum = 0

// Iterate over the array
for (i = 0; i < array.length; i++)
{
  // add current index to sum
  currentSum = currentSum + array[i]

  if(currentSum > maxSum)
  {
    maxSum = currentSum;
  }
  // Is the current sum less than zero?
  if(currentSum < 0)
  {
    // Reset the sum and subarray indexes.
    currentSum=0
  }
}
return maxSum
}

Now imagine an array where ALL of the values are MIN_INT. With the maxSum now set to the minimum value for an integer any value in the array is guaranteed to be greater than or equal to the maxSum. If the first value in the array is the MIN_INT then the maxSum will remain MIN_INT. The currentSum will be reset to 0. At each iteration, the value of currentSum will be found to be less than or equal to the maxSum and therefore the maxSum will not change.

After all of the array values have been inspected the maxSum of MIN_INT will be returned.

If there is an array where at least one of the values is greater than MIN_INT then the currentSum will be greater than maxSum and it will be set accordingly.

You now can compute the maximum sum sub-array in O(n) time and process an array with all negative values or a mix of negative and positive.

The problem presented is that you have a one dimensional array of numbers. From that array you need to find the maximum sum sub-array. The sub-array must be contiguous.

The solution to this can be in several forms. You could just want the actual maximum sum of the numbers. In this case you would find the sub-array and then sum all of the numbers and return the value of the maximum sum. Another solution could be that you want the elements of the sub-array. Finally, perhaps you just need to provide the indices where the sub-array starts and ends.

There are several ways you can implement this solution.

• Brute-force. Just look at every possible combination and choose the best one.
• Divide and Conquer. This approach will divide the problem into a smaller problem and solve the smaller problems.
• Kadane's algorithm

Here we explore the Brute-Force method.

Brute Force Sum

Whenever I am trying create a solution, the brute-force method is one of the first things I do. It certainly is not the best, but it can be an effective way to better understand the problem and ensure you are getting a correct solution.

The concept behind the brute-force method is that you will just try all of the possible solutions until you are satisfied that you have the best.

Brute force algorithms are rarely the best. Sometimes they are the only method available for a problem. This is not the case for this problem though.

Using the array [-1, 3, -2, 3, -2, -1, 5, -4, -1] the maximum sum sub-array of [3, -2, 3, -2, -1, 5] starting at index 1 and ending at index 6 with a sum of 6.

A brute force approach to finding this value would be to iterate over the array and keeping track of each sub-array and the sum. If a sum is found that is higher you keep track of that.

maxSum=0
currentSum=0

for(i=0; i < array.length; i++)
{
  currentSum=0
  for(j=i; j < array.length; j++)
  {
    currentSum = currentSum + array[j];
    if(currentSum > maxSum)
    {
        maxSum = currentSum;
    }
  }
}
return maxSum;

In the pseudo-code we start at the first position in the array and reset the current sum. The first check inside the second loop looks at the value of the sub-array starting at index 0 and of a size of 1.

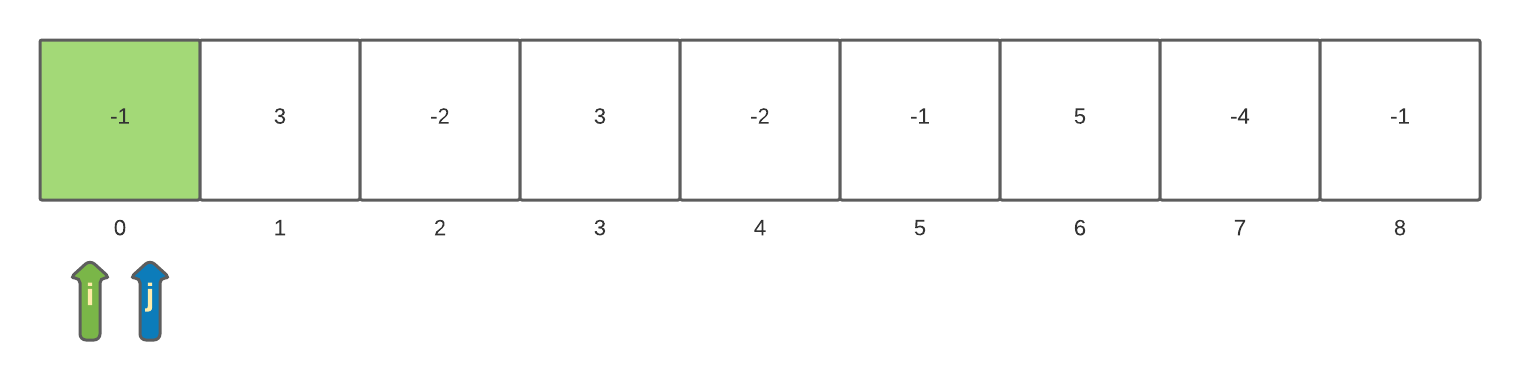
The first time through the loop with i=0 and j=0 the sum is -1. Since -1 is less than the current maxSum it will not be assigned to maxSum

The end index j will be incremented to 1 and point to the next element in the array. This increases the size of the current sub-array to 2.

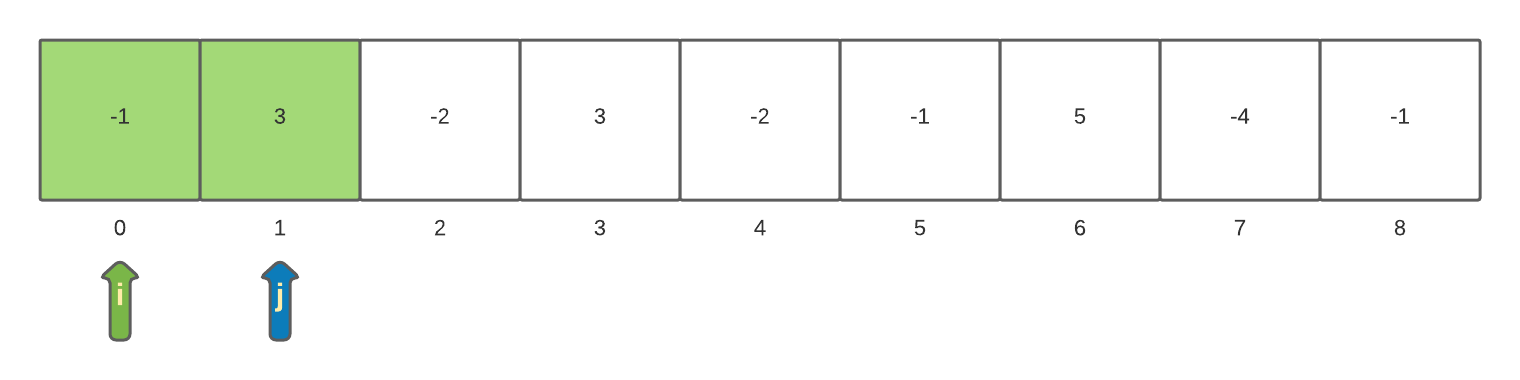
The value of the array[j] is now added to the currentSum and currentSum becomes 2. The currentSum is compared against the maxSum. Since the current currentSum is greater than the maxSum the maxSum is updated to be the value of currentSum.

The inner loop continues to increment the index value of j and add the value of array[j] to the currentSum. Each time the currentSum is incremented it is compared against the value of maxSum. If the value of currentSum is greater than maxSum it will become the new maxSum.

This results in the maxSum changing during the initial loop of j to 3 and then 5 before reaching the end of the array.

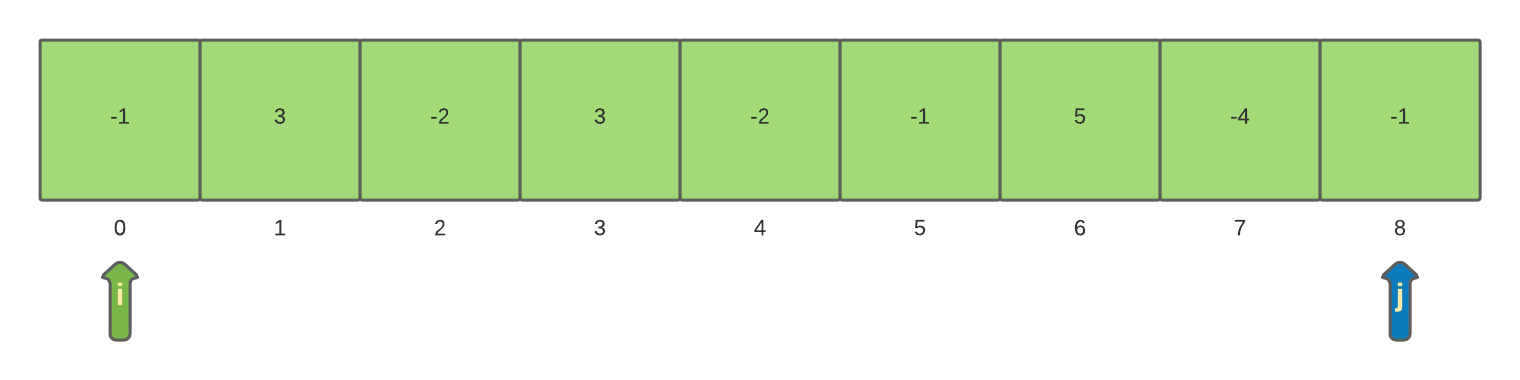
Now that the inner loop has completed to the end of the array the outer loop iterator i is incremented to 1 and the currentSum is reset to 0. At this time the maxSum is 5. Now the process of examining a sub-array and the sum resumes. However, this time the sub-array will start at position 1.

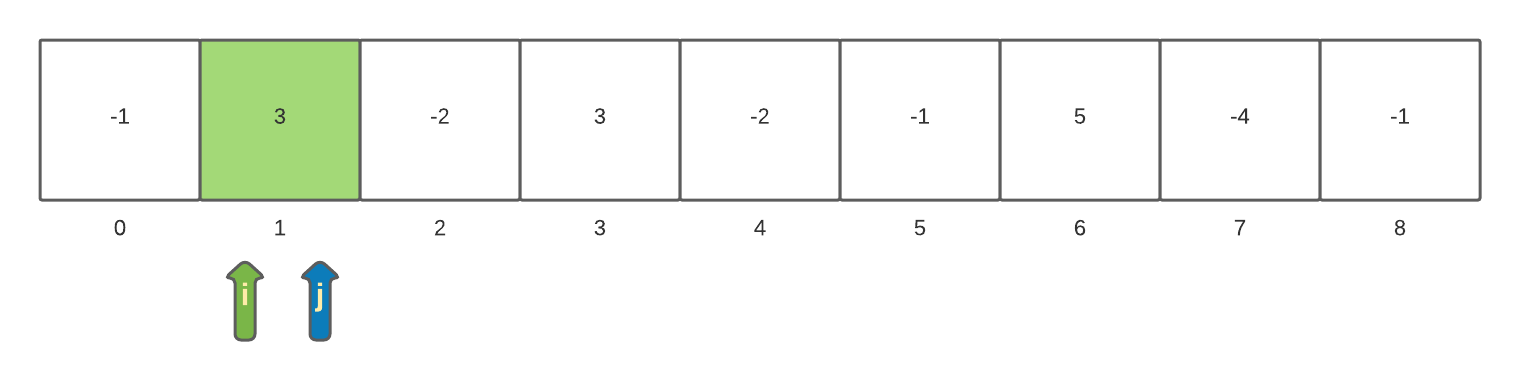
The process of incrementing the inner loop iterator and incrementing the currentSum will continue until the inner loop reaches the end of the array. When we reach the ending index inside the inner loop with a value of 6 we find the next maxSum of 6.

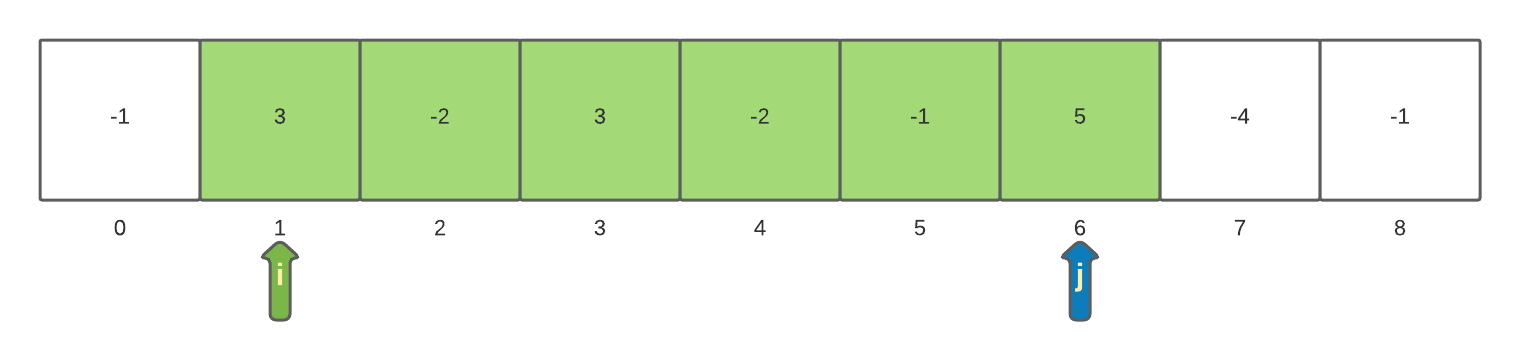
The inner loop continues to be incremented until it again reaches the end of the array. The final scan of a sub-array starting at index 1 results in a sub-array of size 8 with a maxSum of 6.

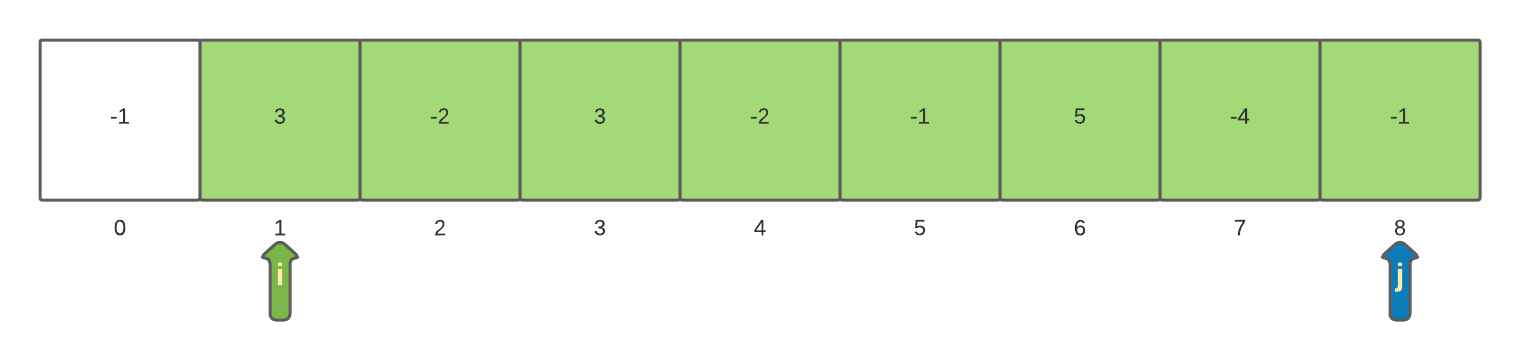
After the scanning the array with position 0 as the starting index and then scanning the array again with the starting position as 1 we have a new maxSum of 6.

The process of incrementing the staring index and then scanning the array until the end continues. Anytime a greater maxSum is found it is saved. Eventually the starting index will be incremented to the very last index in the array and the final sub-array to be tested will be a sub-array of size 1 starting at index 8.

At this point every possible sub-array has been tested and the maximum sum has been determined.

Analysis of Solution

The time complexity of the solution depends on the loops. The inner loop must iterate over the array N times. This means that the number of iterations depends on the number of elements in the array.

The outer most loop must also iterate over the array N times. Since the second loop is nested inside the outer loop this makes the complexity N*N. This is expressed as O(n^2).

The next thing to consider is the amount of space, or memory, that is required to complete the solution. In this solution we have to initialize a few variables, but the size of those variables is constant. The size of the incoming array is also constant. The amount of memory used in this solution remains constant during the entire process. This makes the space complexity O(1).

What about all negative numbers?

After running some sample data through this algorithm you might notice that there are some edge cases that do not work. The first one is when you have an array that contains all negative numbers. The current algorithm doesn't seem to handle it very well. It reports that the maxSum is zero depsite there being no way to have that value if all of the numbers are negative.

This can be easily fixed.

Instead of initializing the maxSum=0, initialize it to the minimum integer value possible.

maxSum=MIN_INT

This simple change will now allow the algorithm to properly report on an array that has all negative numbers.

What is the actual sub-array

Another aspect of the current algorithm is that you cannot actually report on what the sub-array is that provides the maximum sum. You only know what that sum is. By iterating through the example we can see that the maximum sub-array is actual the array starting at index 1 and ending at index 6.

To be able to provide this information as a result of the algorithm we need to make some minor changes. We need to track what the beginning and ending indexes are. We can do this by adding a few extra variables.

maxStartIndex = 0
maxEndIndex = 0

Initially we assign the values to zero. Each time we find a currentSum that is larger than the maxSum we assign the index values. This results in the outer loop iterator i being assigned to the maxStartIndex and the inner loop iterator j being assigned to maxEndIndex.

We now know at the end of all of the scans that the start and end index is for the sub-array that results in a maximum sum.

Using this information a new sub-array can be returned or just the indexes of the sub-array can be returned.

When using HttpClient.SendAsync() to access a resource that might take a while to process it can be advantageous to detect when the connection has been disconnected.

This can be done using a CancellationToken passed to the HttpClient.SendAsync() method.

public class HttpRequestHandler : IHttpRequestHandler
{
    public CancellationToken CancellationToken => _cancel;

    public HttpRequestHandler(IHttpContextAccessor httpContext)
    {
        _cancel = httpContext?.HttpContext?.RequestAborted ?? CancellationToken.None;
    }

     /// <summary>
    /// Execute request and return response.
    /// </summary>
    public virtual async Task<IResponse<T>> ExecuteAsync<T>(IRequest request) where T : class, new()
    {
        // ...
        var response = await this.GetClient(request).SendAsync(request1, completionOption, CancellationToken).ConfigureAwait(false);
        // ...
    }
}

Anytime a connection to a long running process is made there is the risk that the connection will be terminated prior to the process completing. A Cancellation Token is used to notify a process that a request should be cancelled.

As part of the connection to an ASP.NET Core Controller there is the HttpContext. This provdes access the a CancellationToken.

To test if the process should cancelled you check the status of the RequestAborted.IsCancellationRequested property within the HttpContext.

[HttpGet]
public async Task<IActionResult> Get(IHttpContextAccessor httpContext)
{
  if(httpContext?.HttpContext?.RequestAborted.IsCancellationRequested)
  {
    // Stop processing
  }
}

The RequestAborted is an instance of a CancellationToken.

Another way to access the CancellationToken is to pass it as part of the Dependency Injection (DI) into the Controller.

[HttpGet]
public async Task<IActionResult> Get(CancellationToken cancellationToken)
{
  // ...
  if(cancellationToken.IsCancellationRequested)
  {
    // Stop processing
  }
  // ...
}

Once the cancellation request has been detected the process should gracefully stop the processing and return.